So based on my last post about Canada’s math wars I had a number of people stop to comment about direct instruction in general, including Robert Craigen who kindly linked to the PCAP (Pan-Canadian Assessment Program).
(Note: I am not a Canadian. I have tried my best based on the public data, but I may be missing things. Corrections are appreciated.)
For PCAP 2010, close to 32,000 Grade 8 students from 1,600 schools across the country were tested. Math was the major focus of the assessment. Math performance levels were developed in consultation with independent experts in education and assessment, and align broadly with internationally accepted practice. Science and reading were also assessed.
The PCAP assessment is not tied to the curriculum of a particular province or territory but is instead a fair measurement of students’ abilities to use their learning skills to solve real-life situations. It measures learning outcomes; it does not attempt to assess approaches to learning.
Despite the purpose to “solve real-life situations” the samples read to me more like a calculation based test (like the TIMSS) rather than a problem solving test (like the PISA) although it is arguably somewhere in the middle. (More about this difference in one of my previous posts.)
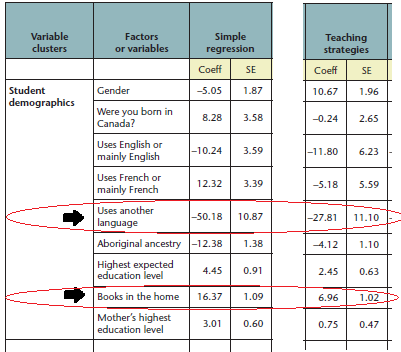
Despite the quote that “it does not attempt to assess approaches to learning”, the data analysis includes this graph:
Classrooms that used direct instruction achieved higher scores than those who did not.
One catch of note (although this is more of a general rule of thumb than an absolute):
Teachers at public schools with less poverty are more likely to use a direct instruction curriculum than those who teach at high-poverty schools, even if they are given some kind of mandate.
This happened in my own district, where we recently adopted a discovery-based textbook. There was major backlash at the school with the least poverty. This seemed to happen (based on my conversations with the department head there) because the parents are very involved and conservative about instruction, and there’s understandably less desire amongst the teachers to mess with something that appears to work just fine. Whereas with schools having more students of poverty, teachers who crave improvement are more willing to experiment.
While the PCAP data does not itemize data by individual school, there are a two proxies that are usable to assess level of poverty:
Lots of books in the home is positively correlated to high achievement on the PCAP (and in fact is the largest positive factor related to demographics) but also positively correlated to the use of direct instruction.
Language learners are negatively correlated to achievement on the PCAP (moreso than any other factor in the entire study) but also negatively correlated to an extreme degree in the use of direct instruction.
It thus looks like there’s at least some influence of a “more poverty means less achievement” gap creating the positive correlation with direct instruction.
Now, the report still claims the instruction type is independently correlated with gains or losses (so that while the data above is a real effect, it doesn’t account for everything). However, there’s one other highly fishy thing about the chart above that makes me wonder if the data was accurately gathered at all: the first line.
It’s cryptic, but essentially: males were given direct instruction to a much higher degree than females.
Unless there’s a lot more gender segregation in Canada than I suspected, this is deeply weird data. I originally thought the use of direct instruction must have been assessed via the teacher survey:
But it appears the data instead used (or least included) how much direct instruction the students self-reported:
The correlation of 10.67 really ought to be close to 0; this indicates a wide error in data gathering. Hence, I’m wary of making any conclusion at all of the relative strength of different teaching styles on the basis of this report.
…
Robert also mentioned Project Follow Through, which is a much larger study and is going to take me a while to get through; if anyone happens to have studies (pro or con) they’d like to link to in the comments it’d be appreciated. I honestly have no disposition for the data to go one way or the other; I do believe it quite possible a rigid “teaching to the test” direct instruction assault (which is what two of the groups in the study seemed to go for) will always beat another approach with a less monolithic focus.
Filed under: Education, Mathematics, Statistics |






Jason, try http://www.ascd.org/ASCD/pdf/journals/ed_lead/el_197803_house.pdf
for starters. The “direct instruction” and Direct Instruction advocates have been citing Follow-Through for decades because they view it as scientific proof that their approach is superior. The above is a re-evaluation of the original findings. I think it does an excellent job of calling those self-serving and highly-questionable conclusions into doubt.
The whole approach one gets from those on the DI side of the aisle is a microcosm of the Math Wars: one side is arrogant and contemptuous, believing it has found the Holy Grail of education and absolutely dismissive of any and all competitors, any and all skepticism that its methods and beliefs are a panacea. On my view, that side wants a rigged game in which it gets to make the rules, change the rules to suit every circumstance, and in particular to pick what gets used for assessment. And even with such advantages, it still has to cheat regularly to sell its ideology and products.
Meanwhile, Project Follow-Through, even if it actually led to the conclusions the DI folks want everyone to accept that it does, is way out of date. Time for something from the 21st century?
As for your comments about affluent schools leaning towards direct instruction: that may be partially true, but it’s also true that affluent districts are free to use far more creative approaches to mathematics: poverty-stricken schools are increasingly stuck with a test-driven approach thanks to No Child Left Behind and its descendents. And some advocates for poor and minority kids have come to the well-intentioned (but on my view erroneous) conclusion that its racist or otherwise wrongheaded to use progressive educational ideas with “needier” kids because, at least in part, they’re getting the short end of the stick on the high-stakes assessments. What they fail to do, as do others, is question the legitimacy of and political agenda behind the assessments themselves. Go back to Follow-Through and ask, as have knowledgeable critics, whether the assessments were chosen with preconceptions and foregone conclusions about what works in mind. In other words, rigging the game to get the desired outcomes, then touting the predictable results for the next half-century. NCLB and its heirs are more of the same, in my view, which is what is among the very worst aspects of the entire Common Core Initiative. And ironically, conservative opposition to CCSSI is coming in part from those who don’t want any sort of assessments that break the simplistic multiple-choice, calculation-driven mold. They also quite openly despise the Standards for Mathematical Practice, which they correctly recognize as grounded in the NCTM Process Standards (even if they never understood those or were able to discuss them honestly). In other words, anything that smacks of progressive educational, student-centered education must be and is consistently opposed.
In the end, I’m convinced that no matter what games the di/DI crowd plays, their interest in the sort of problem-solving that PISA may be measuring better than TIMSS or domestic high-stakes tests in the US and elsewhere is minimal. It’s always been and always will be about calculation uber alles. They will denigrate problem-solving and assessments that focus upon it. They will claim that problem-solving “can’t be taught.” They will remain married to a behavioral psychology view of education that promises to do little or nothing for vast numbers of students while maintaining the status quo for the advantaged (who remain free to get all sorts of lovely enrichment programs inside or outside of school, because their parents can afford them and are willing to pay for them).
Despite all the wailing by these educational conservatives and reactionaries, the fact is that progressives have yet to have their innings because they’ve never had control of assessment. It’s as if every match must be played on the home turf of the traditionalists, with their rules, their equipment, their judges and officials, and their scorekeeping. As the saying goes, “Nice work if you can get it.” And they have been able to, for decades. It’s time for that to change.
In my experience here in BC, teaching is rarely gender-segregated outside of (expensive) private schools. I have seen the odd gender-split class in middle school but it’s the exception.
If male students are self-reporting a lot more DI than female students, that seems to say more about how students perceive their classroom experience than on what the teachers are actually doing.
Josh, of course you might be right about male perception and self-reporting. Seems like it would make far more sense to have data based on a rubric and reporting by trained observers.
It’s now been about 11 years since I had a conversation at the NCTM Annual Meeting Research Presession with James Hiebert (of THE TEACHING GAP fame) on the question of how much math teaching in the US fit what might be called NCTM-Standards-based instruction. He posited that if we were to drop a pin randomly on a map of the US and then observe in the closest school district, the probability of finding such instruction was about 0.
Given the influence of NCLB and its heirs, I find it impossible to believe that things have swung significantly away from skills-based, computationally-focused, test-driven teaching. If anything, fewer districts are committed to going with anything at all inquiry-oritented or student-centered.
The one ray of hope I’ve seen is based on the evidence of the math teachers who blog actively and who seem to be collectively determining their own path for math content and pedagogy. Dan Meyer is one of the hubs of that movement, but it doesn’t depend upon Dan or any single individual. Too many good, motivated, bright, creative people have discovered that they have like-minded colleagues they can access daily even if they teach hundreds or thousands of miles away from them. So the ‘Net may ultimately be the saving grace for inspired and inspiring mathematics teaching. As for learning, I continue to hope that free online instruction will give millions of kids and adults access to great mathematics teaching and problem-solving. James Tanton, Herb Gross, and many others have given us fabulous free resources to watch and participate in. That sort of thing can only grow, Sal Khan and his “academy” notwithstanding (sorry, but I find his stuff part of the problem, not part of the solution).
The disagreement about DI and constructivism seems to be more philosophical than scientific, so arguing is unlikely to help. Instead, I would like to shift the narrative to pedagogies that may appeal to people on both sides of the debate and haven’t received as much attention. Here are my favorites:
1. Case Comparison
One meta-analysis has found that comparing examples/cases and attempting to abstract the underlying idea is highly effective for learning in math and science. For example, comparing two different solution procedures and mathematical expressions helps students understand which solution method to use and when.
http://bit.ly/1NKf6Rh
2. Representational Sequencing
The “concreteness fading” method of instruction, echoing Bruner, recommends beginning with concrete explanations/representations and slowly fading them into abstractions. It synthesizes the best of concrete and abstract teaching. However, some researchers have found that the reverse sequence (moving from abstract explanations to concrete ones) is helpful in domains like engineering (likely because starting with the complex concrete representation may burden learners) .
http://bit.ly/1J1Fsus
http://bit.ly/1eAPevi
3. Gesturing and Embodied Teaching
Gesturing during teaching and learning has a positive effect on learning math and other subjects. Engaging the body in learning has wide-ranging effects.
http://1.usa.gov/1UujER4
http://bit.ly/1H8o5ql
It’s disappointing to read posts about “the math wars” and direct instruction considering the richness of education science right now. Let’s find some time to discuss innovative practices that more people can agree on.
#1 came up with my cognitive load theory post and #2 came up when I posted about Abstract and concrete simultaneously.
I have only delved into Math Wars ™ stuff recently due to current events. Normally I prefer cognitive science and design related to education to this beat, but it’s hard to avoid the politics sometimes. You wouldn’t think abstract vs. concrete would get political, but they have; see my post from my old blog Concrete Examples As Rhetorical Device.
To be clear, I think this blog coverage of instructional methods is better than others.
If the debate still interests you, this study may help you understand the DI/discovery debate :
https://www.dropbox.com/s/bha0v5o1ktwqlbl/Inventing%20a%20Solution.pdf?dl=0