On the Ancient Egyptian Value for Pi

Do a little searching on the Internet, and you’ll find the ancient Egyptian value for given as 3.16. Do a little more searching and you might get the more exact answer of .

Where did these numbers come from? How did Egyptians discover the procedure for working with circles in the first place? And finally, did the Egyptians really know anything about , or was this a later extrapolation?

The document that gets used to find is the Rhind Mathematical Papyrus (1650 BC); sometimes it’s known as the A’h-mosè Papyrus depending on if you’re naming it after the person who purchased it or the person who wrote it. I personally prefer the actual title given by the author,

Directions for Attaining Knowledge of All Dark Things

but to be consistent with mathematical historians I’ll call it the RMP, for Rhind Mathematical Papyrus.

The RMP itself is divided into 87 problems. (The last three are enigmatic and mangled and may not be problems at all, so sometimes the count is given as 84.) The problem we’re looking at here is #50, the second one on this page.

The translation goes roughly

Example of finding the area of a round field with a diameter of 9 khet. What is its area?

Take away 1/9 of its diameter, namely 1. The remainder is 8.
Multiply 8 times, making 64. Therefore the area is 64 setjat.

(1 khet = about 52.3 meters = about 57.2 yards)

If you like, you can try to work out this point how comes about. You need to compare the formula the Egyptians get with the circle area formula of . Come back when you’re ready.

Given a diameter of 2r, 1/9 of it is

So “cut off” 1/9 of the diameter we subtract from the original diameter

And we’re left with

Turning that length into the side of a square, the area is the expression squared

With simplification it becomes

Voila, by matching this formula with , out comes a value of 256/81 for .

That’s lovely, but how did the Egyptians know that such a strange procedure would get the right area? It’s possible they came up with it using raw experimentation, but there’s a hint one page back in the manuscript of what the Egyptians were really up to.

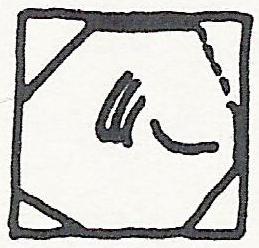
This is from problem 48, which is a touch enigmatic. There’s no stated goal, just the calculation, which gives the area of the square as 81, and the area of the circle (octagon?) on the inside as 64.

Whether the figure is an octagon or a circle is up for some debate. Richard Gillings argues it is an octagon, because the other circles that show up in the manuscript (like for #50) are obviously drawn as circles, but it’s possible the author affected a different stroke because the figure is inscribed within a square. I’m going with circle, because an area of 64 for the octagon isn’t just approximate, it’s wrong.

(The argument that follows is also courtesy Richard Gillings.)

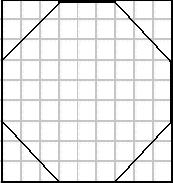
Even using the simplest of methods (just count!) it isn’t hard to find an area of 63 for the octagon. Noting that a circle isn’t too far off from the octagon

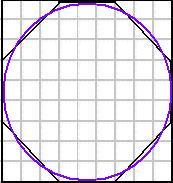
and that the 18 missing squares can be arranged (with one overlapping) like so

It’s quite possible to imagine the area of the circle as the approximate area of the 8 by 8 square remaining.

The question I want to raise about all this is: did the Egyptians really know anything about at all? Is it fair to compare what they did to Newton’s 15 digits, when the presumed value is extrapolated from a single procedure in the RMP?

In the Indian text Sulba Sutras there is a different value for the area procedure and the circumference procedure. I argue the Egyptian achievement is comparable — it’s a procedure, not actual knowledge of the ratio — and the caveat needs to be noted in histories of the number.